Un histogramme est une représentation graphique d'une distribution de données. En d'autres termes, il s'agit d'un graphique qui montre combien de points de données entrent dans chaque catégorie.
Dans les affaires, l'économie et d'autres disciplines, les histogrammes peuvent fournir un outil utile pour analyser les données et les tendances. Ils sont utilisés lorsque vous souhaitez voir comment les données sont distribuées et la fréquence d'occurrence d'un événement ou d'une propriété mesurable.
Mais exactement quand un histogramme doit-il être utilisé ? en affaires ou dans une autre discipline?
Voici quelques-uns des cas d'utilisation et applications les plus importants de l'histogramme :
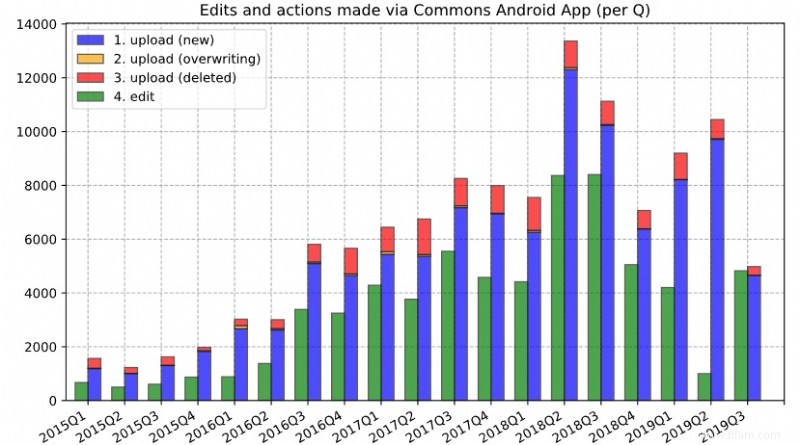
Histogramme de site Web téléchargements . Photo : Misaochan / Wikimédia.
Un histogramme est une représentation graphique de la distribution des données . Il est utilisé lorsque les données ont un seul indépendant variable .
La variable indépendante est la variable qui est manipulée par le chercheur, tandis que la variable dépendante est la variable qui est mesurée.
Ainsi, un histogramme peut être utilisé pour déterminer la forme de la distribution, le centre de la distribution et la propagation de la distribution.
Il peut également être utilisé pour comparer les distributions de deux ou plusieurs ensembles de données.
Un histogramme est mieux utilisé lorsque les données ont une plage continue. En effet, un histogramme peut afficher la distribution des données avec plus de précision qu'un graphique à barres.
Dans un histogramme, la surface de chaque barre est proportionnelle à la fréquence des données qu'elle représente. Cela permet de voir facilement la distribution des données.
Les histogrammes sont un excellent outil pour comparer la distribution de fréquence de deux ensembles de données. Les deux ensembles de données peuvent être identiques , ou ils peuvent être différents. Ils peuvent appartenir à la même population ou à des populations différentes.
Pour comparer la distribution de fréquence de deux ensembles de données, vous devez d'abord créer des histogrammes pour chaque ensemble de données. Ensuite, vous devez comparer les deux histogrammes.
La façon la plus courante de comparer des histogrammes consiste à utiliser un outil de comparaison d'histogrammes ou un outil de chevauchement d'histogrammes. C'est l'un des meilleurs moyens de comparer la distribution de fréquence de deux ensembles de données.
Beaucoup de gens ne réalisent pas à quel point les histogrammes sont puissants et polyvalents pour l'analyse des données. En particulier, les histogrammes sont particulièrement utiles pour analyser la distribution de fréquence des données d'échantillon.
Bien que les histogrammes soient le plus souvent utilisés pour analyser les distributions de fréquences, ils peuvent également être utilisés pour analyser d'autres types de distributions, telles que la distribution normale.
En particulier, les histogrammes peuvent être utilisés pour déterminer la forme de la distribution, le centre de la distribution et la propagation de la distribution.
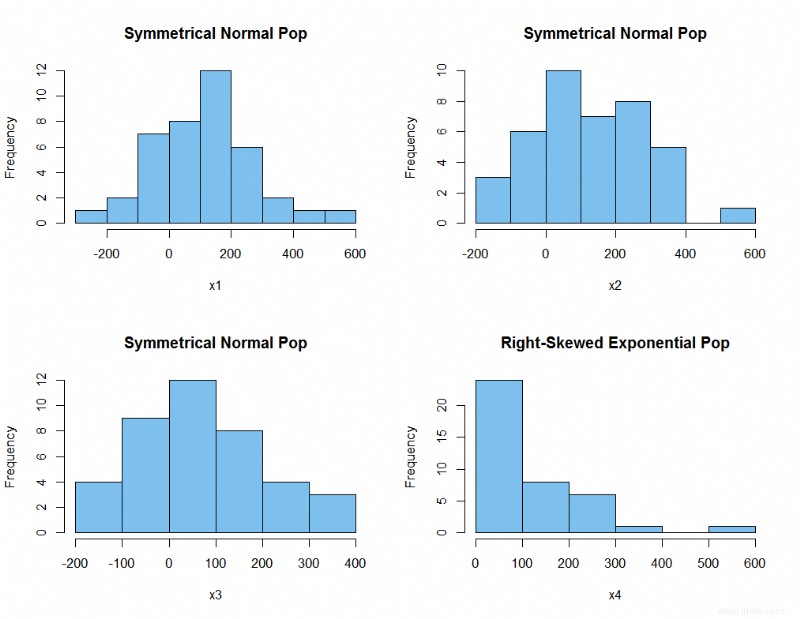
Il existe trois principaux types de distribution : symétrique , incliné à gauche , et oblique à droite . Une distribution symétrique a une moyenne qui se situe exactement au milieu de la plage de données.
Une distribution asymétrique à gauche a une moyenne située à gauche de la plage de données, et une distribution asymétrique à droite a une moyenne située à droite de la plage de données.
Une distribution uniforme a une moyenne qui se situe autour du milieu de la plage de données, mais les groupes ont presque le même nombre de points de données. Cette distribution n'est pas courante. La plupart des distributions sont symétriques ou asymétriques.
Les histogrammes sont utilisés pour analyser comment les résultats du processus changent et peuvent être utilisés pour identifier et corriger les problèmes.
Par exemple, si un histogramme montre que la plupart des points de données sont regroupés autour du milieu de la plage, cela peut indiquer que le processus ne produit pas de résultats cohérents. Alternativement, si les données sont réparties sur une large plage, cela peut indiquer que le processus produit des résultats incohérents.
Les histogrammes peuvent également être utilisés pour déterminer la variabilité des données. Cela se fait en calculant l'écart type, qui est une mesure de la répartition des données. L'écart type est calculé en prenant la racine carrée de la moyenne des différences au carré entre chaque point de données et la moyenne.
Étant donné que les histogrammes peuvent être utilisés pour déterminer la variabilité des données, ils peuvent être utilisés pour identifier et corriger les problèmes d'un processus, que ce soit en entreprise ou dans un autre domaine.