Comme nous le savons tous, l'argent gratuit n'existe pas. Que vous soyez un investisseur ou un consommateur domestique, il y aura des occasions où vous aurez besoin d'emprunter des fonds pour des investissements et des achats. Le coût associé à l'emprunt d'argent est appelé « intérêt ». En tant qu'emprunteur, vous devez comprendre la différence entre l'intérêt simple et l'intérêt composé , afin que vous sachiez exactement combien d'argent vous coûtera en fin de compte. Ce guide décomposera les intérêts simples et composés et la différence entre les deux types.
Les intérêts sont ce qui vous est facturé lorsque vous empruntez de l'argent. Le plus souvent, des frais d'intérêt vous sont facturés lorsque vous contractez un prêt auprès d'une banque ou effectuez des achats avec une carte de crédit. Il est souvent exprimé en APR, qui signifie taux annuel en pourcentage. Lors de la souscription d'un prêt, deux principaux types d'intérêts peuvent être appliqués :les intérêts simples ou les intérêts composés. Continuez à lire pour découvrir la différence entre l'intérêt simple et l'intérêt composé.
[ Vous voulez vous constituer un patrimoine plus rapidement ? Suivez un cours de formation en ligne de 90 minutes pour apprendre à vous désendetter, à augmenter vos revenus et à prendre votre retraite en franchise d'impôt ! ]

Une institution financière peut calculer les intérêts de deux manières :les intérêts simples et les intérêts composés.
Intérêt simple est calculé en utilisant uniquement le montant principal du prêt.
Intérêt composé est calculé en utilisant le montant principal du prêt, plus les intérêts accumulés au cours des périodes précédentes.
La principale différence entre l'intérêt simple et l'intérêt composé est le montant des intérêts que vous finirez par payer sur la durée d'un prêt. Vous pouvez prendre son nom comme indice; l'intérêt simple est plus facile à comprendre et à calculer que son homologue. Étant donné que vous ne payez que des intérêts sur le montant principal du prêt, l'intérêt simple est l'option la plus abordable pour les emprunteurs.
Les intérêts composés augmenteront rapidement votre solde impayé, car vos intérêts accumulent leurs propres intérêts. En tant qu'emprunteur, vous voudrez éviter autant que possible les intérêts composés. Par exemple, les cartes de crédit sont associées à des taux annuels en pourcentage (APR) élevés ou à des intérêts composés annuellement. Les emprunteurs se retrouvent souvent dans l'eau chaude lorsque leurs intérêts semblent s'accumuler plus rapidement qu'ils ne peuvent rembourser le principal.
D'un autre côté, le taux de croissance rapide associé aux intérêts composés est une excellente nouvelle pour les prêteurs et les investisseurs. C'est un outil puissant pour créer de la richesse lorsque vous pouvez l'utiliser à votre avantage.
Voici quelques exemples qui montrent comment les intérêts simples et composés s'accumulent différemment :
Certificat de dépôt : Vous avez un CD de 3 000 $ sur 5 ans qui rapporte un intérêt simple de 1 %. Au cours des 5 années, vous recevrez 150 $. Si le CD était composé mensuellement, vous recevriez plutôt 153,75 $.
Réinvestissement des dividendes : Disons que vous avez acheté 100 actions d'une société. Le dividende est de 3 $ par action. Vous recevrez 300 $ en dividendes, que vous pourrez réinvestir pour acheter plus d'actions. Au fil du temps, acheter et détenir plus d'actions augmenterait vos versements de dividendes.
Investissement d'achat et de conservation : Le rendement boursier annuel moyen est d'environ 10 %. Si vous vous êtes engagé à investir 300 $ par mois pendant 10 ans, les intérêts composés aideraient votre portefeuille à atteindre 58 152,85 $. Avec un investissement total de 36 000 $, vous auriez gagné plus de 22 000 $ en intérêts.
[ Vous voulez vous constituer un patrimoine plus rapidement ? Suivez un cours de formation en ligne de 90 minutes pour apprendre à vous désendetter, à augmenter vos revenus et à prendre votre retraite en franchise d'impôt ! ]
Étant donné que les intérêts simples ne sont calculés qu'à partir du principal du prêt, ils sont faciles à calculer. Pour calculer l'intérêt simple, utilisez la formule suivante :
Intérêt simple =P x r x n
Dans ce cas, la variable P est votre montant principal, r est votre taux d'intérêt annuel et n est la durée du prêt, exprimée en années.
Tout ce que vous avez à faire est de prendre le capital de votre prêt et de le multiplier par votre taux d'intérêt, puis de multiplier le nombre obtenu par le nombre d'années pendant lesquelles vous contractez le prêt. Nous allons vous montrer quelques exemples dans la section suivante.
Exemple 1
Disons que vous empruntez 10 000 $ à la Banque A pour financer l'achat d'une automobile. On vous a cité un taux d'intérêt simple de 5 %, avec une durée de prêt de 5 ans. Le montant des intérêts simples que vous paierez, en plus du capital de 10 000 $, sera de 2 500 $ :
10 000 $ x 0,05 x 5 =2 500 $
Exemple 2
Dans cet exemple suivant, disons que vous contractez un prêt personnel pour l'achat de votre première maison auprès de votre famille. Ils vous prêtent gracieusement 40 000 $ à un taux d'intérêt de 2 %. Ils disent que vous pouvez le rembourser lentement au cours des 10 prochaines années. Vous finirez par payer 8 000 $ d'intérêts dans cette transaction.
40 000 $ x 0,02 x 10 =8 000 $
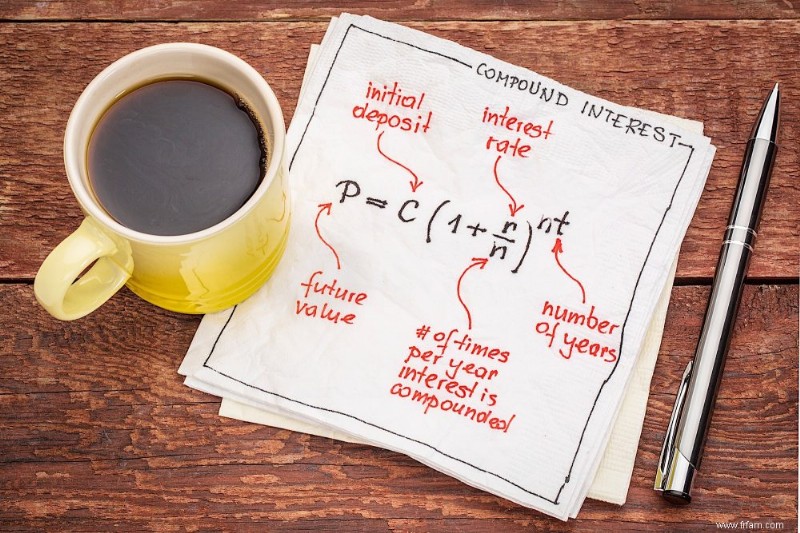
L'intérêt composé est un peu plus complexe que son homologue, l'intérêt simple. Encore une fois, les intérêts composés s'accumulent et s'ajoutent à tout intérêt déjà accumulé au cours des périodes précédentes. En d'autres termes, l'intérêt gagne son propre intérêt. La formule des intérêts composés ressemble à ceci :
Intérêt composé =P[(1+r)^n – 1]
Dans la formule ci-dessus, P est le principal total, r est le taux d'intérêt et n est la durée du prêt, exprimée en années. Vous calculez l'intérêt composé en multipliant le principal du prêt par un plus le taux d'intérêt, qui est porté au nombre d'années du prêt moins un. Vous pouvez également définir une période composée différente pour savoir combien d'intérêts composés vous aurez gagnés à tout moment de la période de prêt. Il est beaucoup plus facile d'expliquer le fonctionnement de cette formule à travers des exemples concrets.
Exemple 1
Utilisons le même exemple que précédemment afin que vous puissiez voir à quel point l'intérêt composé augmentera le total de votre remboursement. Cette fois, vous contractez un prêt de 10 000 $ auprès de la Banque A, mais le taux d'intérêt de 5 % est composé. La durée du prêt est toujours de 5 ans. Dans ce cas, vous finirez par rembourser 2 762,82 $ en intérêts composés. Dans l'exemple précédent, l'intérêt simple était de 2 500 $. Le taux composé augmente votre remboursement d'intérêts de 262,82 $
10 000 $[(1+.05)^5 - 1] =10 000 $ (0,27628)
Exemple 2
Encore une fois, reprenons l'exemple 2 ci-dessus et remplaçons le taux d'intérêt simple par un taux d'intérêt composé. Votre famille vous prête 40 000 $ remboursables en 10 ans. Cependant, cette fois, ils vous demandent un intérêt de 2 % sur ce prêt, à capitaliser annuellement. Au lieu d'un remboursement d'intérêts de 8 000 $, ce serait 8 759,78 $ lorsqu'il est composé chaque année. C'est environ 760 $ de plus qu'avant.
40 000 $[(1+.02)^10 - 1] =40 000 $ (0,21899)
Il existe quelques concepts importants en matière d'intérêt composé. Ces concepts aident à montrer comment votre argent croît, ce que vaut vraiment votre intérêt composé, et plus encore. Nous allons passer en revue le concept de valeur temporelle de l'argent, ainsi que la règle de 72.
Le concept de valeur temporelle de l'argent suit la règle générale selon laquelle "un dollar aujourd'hui vaut plus qu'un dollar demain". Les formules pour trouver la valeur actuelle et la valeur future se trouvent ci-dessous :
Valeur actuelle =valeur future / (1 + i)
Valeur future =valeur actuelle x (1 + i)
Légende :
i =Taux d'intérêt en pourcentage
n =Nombre de périodes de capitalisation dans une année
t =Nombre total d'années pour l'investissement
La règle de 72 vous aide à déterminer quand un investissement doublera de valeur. Cette formule vous oblige à entrer le taux de rendement ou d'intérêt sur l'investissement, et elle suppose également que la capitalisation n'est effectuée qu'une fois par an. Utilisez simplement la formule (72/intérêt) et vous saurez combien d'années il faudra pour que votre investissement double. Par exemple, si votre taux de rendement annuel est de 10 %, votre formule serait (72/10), ce qui équivaut à 7,2 ans avant que votre investissement ne soit doublé.
Enfin, parlons du taux de croissance annuel composé, ou CARG. CARG est utilisé lorsque vous avez besoin de trouver un taux de croissance unique sur une certaine période de temps. La meilleure façon de vous montrer comment cela fonctionne est avec un exemple de calcul. Pour notre exemple, nous dirons que votre investissement a commencé à 20 000 $ et qu'il est passé à 32 000 $ sur une période de 10 ans. Pour calculer notre CARG, nous prendrions la valeur actuelle (20 000 $), la valeur future (32 000 $) et le nombre de périodes de capitalisation (10). Nous insérons ensuite simplement ces chiffres dans notre calculatrice financière ou une feuille de calcul et nous trouverons la valeur de "i". Pour cet exemple, la valeur de "i" est de 4,81 %, ce qui signifie que notre taux de rendement annuel était de 4,81 % sur cet investissement.
Comme vous l'avez appris de nos exemples ci-dessus, il est très important de comprendre la différence entre l'intérêt simple et l'intérêt composé. Les intérêts composés s'accumulent beaucoup plus rapidement que les intérêts simples et peuvent entraîner des centaines de dollars supplémentaires en remboursement d'intérêts. En tant qu'emprunteur, les intérêts composés peuvent jouer contre vous. Cependant, gardez à l'esprit que vous profiterez de ses avantages si vous pouviez plutôt investir ou prêter. Lorsque les finances sont en jeu, c'est toujours une bonne idée d'analyser le pour et le contre et de comprendre dans quoi vous vous embarquez.
Vous voulez vous constituer un patrimoine plus rapidement ?
Cliquez sur la bannière ci-dessous pour suivre un cours de formation en ligne de 90 minutes et apprendre à vous désendetter, à augmenter vos revenus et à prendre votre retraite en franchise d'impôt !
[]